作業十二

蔡智鴻 B94611037
本人5/31曾來上課
部落格
圖片皆在部落中http://kaohsiungman888.blogspot.com/
==========================================
一組標準全齒輪齒輪之徑節為8（亦可使用自設值），齒數分別為30T與48T，其工作壓力角為20度（可為14.5或25度，自選）。
1.試求其接觸線長度，與接觸比。
2.兩齒輪之節圓、基圓直徑各為如何？請列式計算其結果。
3.此組齒輪是否會產生干涉現象？試列式證明之。
4.可否利用draw_gear.m繪出其接合情形，並繪出其動畫效果。
===========================================
1.1.試求其接觸線長度，與接觸比。

===========================================
本題引用contact_ratio程式做計算
輸入[c_ratio,c_length,ad,pc,pb,d2,d3,ag]=contact_ratio(8,30,48,20 )
c_ratio =1.7005%其接觸比=1.7005
c_length =0.6275%接觸長度=0.6275吋
ad =0.1250%齒冠=0.1250吋
pc =0.3927%周節=0.3927
pb =0.369%基周節pb=0.3690
r2 =3.7500%齒輪節圓直徑齒輪一=3.75吋
r3 =6%齒輪節圓直徑齒輪二=6吋
ag =10.4850%齒輪一之接近角=10.4850度
ag =9.9211%遠退角=9.9211度
ag =20.4061%作用角=20.4061度
ag =6.5532%齒輪二之接近角=6.5532度
ag =6.2007%遠退角=6.2007度
ag =12.7538%作用角=12.7532度

另可討論工作壓力角為14.5或25度

工作壓力角為14.5

c_ratio =
2.0308
c_length =
0.7721
ad =
0.1250
pc =
0.3927
pb =
0.3802
d2 =
3.7500
d3 =
6
ag =
12.6898 11.6797 24.3695 7.9311 7.2998 15.2309

工作壓力角為25

c_ratio =
1.5028
c_length =
0.5349
ad =
0.1250
pc =
0.3927
pb =
0.3559
d2 =
3.7500
d3 =
6
ag =
9.1921 8.8419 18.0340 5.7450 5.5262 11.2712

==========================================

1.2.兩齒輪之節圓、基圓直徑各為如何？請列式計算其結果。 　

==========================================
兩齒輪之節圓直徑
由課本定義知

節徑*徑節=齒數

基圓直徑=節徑*cos（壓力角）
所以

齒輪一之節徑為30/8=3.75吋
齒輪二之節徑為48/8=6吋
齒輪一之基圓直徑為3.75*cos(20)=3.523吋
齒輪二之基圓直徑為 6*cos(20)=5.638吋
====================================
1.3.此組齒輪是否會產生干涉現象？試列式證明之。

=====================================
由講義9.47式　

N2及N3要滿足下式才不發生干涉
(N2^2+2N2*N3)sin^2(壓力角) >= 4(1+N3)
依老師所給的條件

假定N2為30,N3為48,壓力角為20

帶入上面的式子
(20^2+2*20*48)sin^2(20) >= 4*(1+48)
271.1 > 196
故本組數據將不會發生干涉

也可以跟isinterf .m 做比較

isinterf(30,48,20)ans = 0

另可討論工作壓力角為14.5或25度

壓力角=14.5°30(30+2*48) sin²14.5°=236.969>4+4*48=196

輸入isinterf(30,48,14.5)

ans = 0

壓力角=25°30(30+2*48) sin²25°=675.13>4+4*48=196

輸入 isinterf(30,48,25)

ans = 0

所以老師給我們的三種壓力工作角情況皆不會產生干涉
===========================================
1.4可否利用draw_gear.m繪出其接合情形，並繪出其動畫效果。

===========================================

本題使用網頁上的draw_gear與move2_gear程式

輸入

draw_gear(8,30,20,360,-2.5,0)

draw_gear(8,48,20,360,2.5,0)

我們可以發現我們我得到的圖，齒輪並沒有互相碰觸在一起

壓力角=20°
move2_gear(8,30,48,20,5)
[輸入]
%第一項為徑節8
%第二項為齒輪一的齒數30
%第三項為齒輪二的齒數48
%第四項為壓力角20
%第五項為齒輪一的角速度10

作業十一

教授抱歉~因為之前作業十的部落格排版一直出問題，

所以延慢了幾天張貼作業十，但是現在問題已經解決了，

所以可否麻煩您再看完作業十一時，往下看一下我的作業十。

造成您的不便深感歉意!!謝謝!!

==========================================

蔡智鴻 B94611037
本人5／24曾來上課部落格
圖片皆在部落中http://kaohsiungman888.blogspot.com/
==========================================
1.某凸輪開始時先在0-100∘區間滯留，然後提升後在200至260∘區間滯留，其高度（衝程）為5公分，其餘l由260∘至360∘則為返程。升程採用等加速度運動，返程之運動型式自定。設刻度區間為10∘，試繪出其高度、速度及加速度與凸輪迴轉角度間之關係。
2.設凸輪之半徑為15公分，以順時針方向旋轉，其從動件為梢型，垂直接觸，長為10公分，從動件之運動係依照第二項之運動型式。
3.試繪出此凸輪之工作曲線。
你能讓此凸輪迴轉嗎？
============================================
1.
假設回程是等速度運動，
輸入指令plot_dwell(0:10:360,5,[2 1],[100 200 260])
%0:10:360 : 指的是圖輪的刻度區有360度而刻度區間是10度
%5 : 從動件衝程[2 1] : 是運動模示2是等加速度運動，1是等速度運動
%[100 200 260] : 指的是運動區間　

除此之外我們還可以把各種狀況都考慮進去
返程等加速度運動(代號2)

返程是簡諧運動(代號3)

返程是擺線運動(代號4)

返程是多項式運動(代號5)

2.
輸入指令[x y]=pincam([0:10:360],15,5,0,10,[100 200 260],[2 1],-1)
%0:10:360 : 指的是圖輪的刻度區有360度而刻度區間是10度
%15 : 凸輪基圓半徑
%5 : 從動件衝程
%0 : 偏置量
%10 : 從動件長度
%[100 200 260] : 指的是運動區間
%[2 1] : 是運動模示2是等加速度運動，1是等速度運動
%-1 : 順時鐘旋轉

3.
使用第三題用到的pincam函式，在裡面多加入一旋轉迴圈，使此凸輪迴轉

所以將老師的pincam改寫為pincamsper

function [x,y]=pincamsuper(cth,r0,s,e,L,range,pattern,cw)

figure(1);%先叫出空白圖

pause(2); %停兩秒，以利準備拍攝的程式

clf;

th=cth*pi/180;

s0=sqrt(r0*r0-e*e);

oo=37;

for nn=1:10:360 mm=nn*pi/180;

oo=oo-1;
clf;
axis([-30 30 -30 30])
for i=1:length(cth)t=th(i)*cw;A=[cos(t+mm) -sin(t+mm);sin(t+mm) cos(t+mm)];

[ym,yy,yyy]=dwell(cth(i),range,pattern);
x0=s0+ym*s;

Sx=[0 x0 x0+L;e e e];

X=A\Sx;x(i)=X(1,2);

y(i)=X(2,2);
end[yw,yww,ywww]=dwell(cth,range,pattern);

y1=yw*s+r0+L;

y2=yw*s+r0 ;
line([0 0],[y1(oo),y2(oo)],'linewidth',10,'color','blue');

line([0 30],[y1(oo),20],'linewidth',10,'color','red');
axis([-30 30 -30 30])

hold on;

plot([0 x],[0 y],'ro',x,y,'k-')
pause(0.02);
end

所以一樣代入函式就可以得到凸輪迴轉的動畫

[x y]=pincamsuper([0:10:360],15,5,0,10,[100 200 260],[2 1],-1)

作業十

蔡智鴻 B94611037本人5／17曾來上課
部落格
圖片皆在部落中http://kaohsiungman888.blogspot.com/
kaohsiungman888.blogspot.com
===============================================
請思考速度與加速度的問題，當一桿以某特定點Ｍ等角速度迴轉時，其端點Ｐ之速度方向如何？其加速度方向如何？

若該特定點Ｍ復以等速水平運動，則同一端點Ｐ之速度與加速度方向會變為如何？

若Ｍ點同時也有加速度，則點Ｐ會有何變化？

若以此推理四連桿的運動，則點Ｐ與Ｑ之速度與加速度方向會與桿一（固定桿）之兩端點之關係如何？

與我們前面的作業分析結果有無共通之處？（參看第六章之四連桿機構之運動分析）
===============================================

請思考速度與加速度的問題，當一桿以某特定點Ｍ等角速度迴轉時，其端點Ｐ之速度方向如何？其加速度方向如何？

假設MP間距離為r(m)　P以等角速度 ω (rad/s)轉動　則依動力學定律，P點切線速度等於r*ω(m/s)，其方向與r為垂直方向　並有向心加速度等於r*ω^2 (m/s^2)

以之前的作業為例

dyad_draw(4,37,.5,0)輸入桿長4, 水平角度37deg, 角速度0.5rad/s

藍色為切線速度 紅色為向心加速度

若該特定點Ｍ復以等速水平運動，則同一端點Ｐ之速度與加速度方向會變為如何？

若M為等速水平運動，則必須再加上VM，所以VP=VM+ωｘｒ，方向則為其向量合，

加速度方面則不受影響，AP= ωｘ(ωxｒ)

若Ｍ點同時也有加速度，則計算Ｐ點加速度時則必須考慮Ｍ點之加速度，AP=AM＋ωｘ(ωxｒ)

若Ｍ點同時也有加速度，則點Ｐ會有何變化？

M點有加速度，所以P點不再只有法線加速度而已，還有一個切線加速度。

和M有水平速度不一樣的地方在於，M有加速度只有影響速度和加速度的大小而已。

AP=AM＋ωｘ(ωxｒ)
若以此推理四連桿的運動，則點Ｐ與Ｑ之速度與加速度方向會與桿一（固定桿）之兩端點之關係如何？與我們前面的作業分析結果有無共通之處？（參看第六章之四連桿機構之運動分析）

固定桿兩端分別為Ｏ點和Ｒ點，此兩點由於接地，其速度與加速度皆為０。

此時我們若以第二桿為驅動桿，則計算Ｐ點速度只需要考慮桿本身的角速度和角加速度，VP=ωop ｘ Rp/o方向與桿２垂直

切線加速度AP=αx Rp/o＋ωop ｘ (ωop x Rp/o)與桿２垂直，法線加速度則沿桿２指向Ｏ點再來我們計算Q點的速度與加速度，這時候則必須要考慮到Ｐ點之速度，Vq=Vp+ωpq ｘ Rq/p =ωq r ｘ Rq/r方向與桿４垂直

切線加速度Aq= Ap＋αx Rq/p＋ωpq ｘ (ωpq x Rq/p) =αx Rq/r+ωqr ｘ (ωqr x Rq/r)與桿４垂直，法線加速度則沿桿４指向Ｏ點　其中上兩式等號最右邊為利用第四桿的角速度與角加速度來計算的，因為Ｒ點為固定點，所以不用考慮Ｒ點本身速度及加速度

================================================
設有一運動之曲柄滑塊連桿組合，設滑塊之偏置量為零，且在水平方向移動，試以此機構之曲桿長度及角度，以及連結桿之長度為輸入項，利用matlab寫出一程式計算在不同曲柄角度時，六點瞬心之對應位置。可順便探討六點瞬心與曲柄角間之關係。
================================================ function drawcenter(r2,th2,r3)
%輸入函數為
%r2 = 曲桿長度
%th2 = 曲桿水平角度
%r3 = 連結桿長度
theta2 = th2*pi / 180;
%首先須記得將th2換算為弧度
X12 = 0; Y12 = 0;
X23 = r2*cos(theta2); Y23 = r2*sin(theta2);
X34 = X23+r3*cos(Y23/r3); Y34 = 0;
X13 = X34; Y13 = X34*tan(theta2);
X24 = 0; Y24 = X34*tan(Y23/r3);
% 繪出各部份
draw_inner = [X12 Y12;X23 Y23;X34 Y34;X12 Y12];
draw_outer = [X34 Y34;X13 Y13;X23 Y23;X24 Y24;X12 Y12];
draw_block = [X34-0.5 Y34-0.5;X34-0.5 Y34+0.5;X34+0.5 Y34+0.5;X34+0.5 Y34-0.5;X34-0.5 Y34-0.5];
hold on;
plot(draw_inner(:,1),draw_inner(:,2),'k-');
plot(draw_inner(:,1),draw_inner(:,2),'bo');
plot(draw_outer(:,1),draw_outer(:,2),'r:');
plot(draw_outer(:,1),draw_outer(:,2),'bo');
plot(draw_block(:,1),draw_block(:,2),'k-');
hold off;
%標註
text(X12+0.2,Y12-0.2,'12');
text(X23+0.2,Y23-0.2,'23');
text(X34+0.2,Y34-0.2,'34');
text(X13+0.2,Y13-0.2,'13');
text(X24+0.2,Y24-0.2,'24');

輸入
for i = 0:360,
clf;
axis([0 100 -10 90])
axis equal
%在此必須固定座標軸

drawcenter(60,i,50);
pause(0.2);
end;

結果如動畫

讓MATLAB實力大增的秘技

挖恭喜你點近來!!
點進去你絕對不會後悔的啦
http://ecatt.badger.ncit.edu.tw/wpd92/92U40/plot.htm

作業九

蔡智鴻 B94611037本人4／26曾來上課
部落格
圖片皆在部落中http://kaohsiungman888.blogspot.com/
=========================================
就教科書中第四章第五節之偏置機構作另類分析，分析過程可採你所知的方式（包括講義中所列的方法）。運動中分以曲桿驅動及滑塊驅動的方式，並說明運動的界限或範圍。設此機構之曲桿長Rcm ， 連桿Lcm，滑塊之偏置量為10cm等數據作分析。其中，R=10+(學號末二碼），Ｌ＝Ｒ+5 。
=========================================
R=10+37=47 L=37+5=52

r(1) 固定桿 第一桿的方向雖然是固定的，但長度卻會隨著機

構的運動而變動，所以可任意設定。

r(2) 曲桿 =47藍色的

r(3) 結合(連)桿=52紅色的

r(4) 垂直偏置量=10

theta1 第一桿之水平角

theta2 驅動桿之水平夾角

td2 驅動桿角速度
tdd2 驅動桿角加速度

sigma 組合模數

driver 驅動桿0代表驅動桿為第二桿。1代表驅動桿為第三桿。2代表由滑塊驅動。

1.利用講義的drawsldlinks來畫出靜態圖

驅動桿為第二桿(driver為0)：
閉合型

drawsldlinks([0,47,52,10],0,90,1,0) %設th1=0度,th2=60度

輸入drawsldlimits([0 47 52 10],0,1,0)

注意：當驅動桿為第二及第三桿時，其Qstart與Qstop分別表示驅動桿之最小及最大角度

Qstart =
3.6000e-006
Qstop =
360.0000

上圖很明顯是錯的，因為上圖的最大角度和講義中的工式顯然不符，而且網路上的講義程式討論中並未提到r3≧r4≧0，且 r3+r4 ≧ r2情況所以若直接用網路上程式計算本題極限角會出錯
所以我在sld_angle_limits 地case 0(曲桿為驅動桿)中加入

elseif

r3+r4＞=r2 & r3＞=r4 & r4＞=0,

Qstart=-asin((r3-r4)/r2);

Qstop=pi+asin((r3-r4)/r2);
如此才能正確計算出極限角度

從新輸入drawsldlimits([0 47 52 10],0,1,0)

Qstart =
-63.3313
Qstop =
243.3313

除此之外我們還可以以動畫來詳細的看他運動的圖形

輸入

i=-63.3313

drawsldlinks([0 47 52 10],0,i,1,0) %叫出此圖形讓我準備拍攝工具

axis([-130 130 -130 130])

pause(3)

for i=-63.3313:10:243.3313%最小角到最大角分10等份

pause(0.3)

clf

drawsldlinks([0 47 52 10],0,i,1,0)

axis([-100 100 -100 100])

end

分支型

drawsldlinks([0,47,52,10],0,90,-1,0) %設th1=0度,th2=60度

輸入drawsldlimits([0 47 52 10],0,-1,0)

Qstart =
3.6000e-006
Qstop =
360.0000

上圖很明顯是錯的，因為上圖的最大角度和講義中的工式顯然不符，而且網路上的講義程式討論中並未提到r3≧r4≧0，且 r3+r4 ≧ r2情況所以若直接用網路上程式計算本題極限角會出錯 所以我在sld_angle_limits 地case 0(曲桿為驅動桿)中加入
elseif
r3+r4＞=r2 & r3＞=r4 & r4＞=0,
Qstart=-asin((r3-r4)/r2);
Qstop=pi+asin((r3-r4)/r2);

如此才能正確計算出極限角度

從新輸入drawsldlimits([0 47 52 10],0,-1,0)
Qstart = -63.3313

Qstop = 243.3313

除此之外我們還可以以連續圖來詳細的看他運動的圖形

輸入
i=-63.3313
drawsldlinks([0 47 52 10],0,i,-1,0) %叫出此圖形讓我準備拍攝工具
axis([-130 130 -130 130])
pause(3)
for i=-63.3313:10:243.3313%最小角到最大角分10等份
pause(0.3)
clf
drawsldlinks([0 47 52 10],0,i,-1,0)
axis([-100 100 -100 100])
end

驅動桿為第二桿(driver為1)：

閉合型

drawsldlinks([0,47,52,10],0,90,1,1) %設th1=0度,th2=60度

輸入drawsldlimits([0 47 52 10],0,1,1)

Qstart =
-45.3602
Qstop =
225.3602

除此之外我們還可以以連續圖來詳細的看他運動的圖形

輸入
i=-45.3602

drawsldlinks([0 47 52 10],0,i,1,1) %叫出此圖形讓我準備拍攝工具
axis([-130 130 -130 130])
pause(3)
for i= -45.3602 :10:225.3602 %最小角到最大角分10等份
pause(0.3)
clf
drawsldlinks([0 47 52 10],0,i,1,1)
axis([-100 100 -100 100])
end

分支型

drawsldlinks([0,47,52,10],0,90,-1,1) %設th1=0度,th2=60度

輸入drawsldlimits([0 47 52 10],0,-1,1)

Ostart =
-45.3602
Qstop =
225.3602

除此之外我們還可以以連續圖來詳細的看他運動的圖形

輸入 i=-45.3602
drawsldlinks([0 47 52 10],0,i,-1,1) %叫出此圖形讓我準備拍攝工具

axis([-130 130 -130 130])

pause(3)

for i= -45.3602 :10:225.3602 %最小角到最大角分10等份

pause(0.3)

clf

drawsldlinks([0 47 52 10],0,i,-1,1)

axis([-100 100 -100 100])

end

滑塊驅動部份(driver為2)：

閉合型

drawsldlinks([0,47,52,10],0,90,1,2) %設th1=0度,th2=60度
輸入drawsldlimits([0 47 52 10],0,1,2)

注意:當驅動件為滑塊時，其不再是角度，而是其對應之桿一最小及最大長度，亦即r1min與r1max。
Qstart =
-98.4937
Qstop =
98.4937

除此之外我們還可以以連續圖來詳細的看他運動的圖形

輸入

i= -98.4937

drawsldlinks([0 47 52 10],0,i,1,2) %叫出此圖形讓我準備拍攝工具
axis([-130 130 -130 130])
pause(3)
for i= -98.4937 :10:98.4937 %分10等份
pause(0.3)
clf
drawsldlinks([0 47 52 10],0,i,1,2)
axis([-100 100 -100 100])
end

分支型

drawsldlinks([0,47,52,10],0,90,-1,2) %設th1=0度,th2=60度

輸入drawsldlimits([0 47 52 10],0,-1,2)

注意:當驅動件為滑塊時，其不再是角度，而是其對應之桿一最小及最大長度，亦即r1min與r1max。

Qstart =
-98.4937
Qstop =
98.4937

除此之外我們還可以以連續圖來詳細的看他運動的圖形

輸入
i= -98.4937
drawsldlinks([0 47 52 10],0,i,-1,2) %叫出此圖形讓我準備拍攝工具

axis([-130 130 -130 130])

pause(3)

for i= -98.4937 :10:98.4937 %分10等份

pause(0.3)

clf

drawsldlinks([0 47 52 10],0,i,-1,2)

axis([-100 100 -100 100])

end

結論:

1.從上面的初始圖我們可以發現，組合模數之閉合或分枝會導致左右鏡像的結果.
2.由上面六張圖可發現此狀況中分支型和閉合型其極限角之位置是相同的

作業八

蔡智鴻 B94611037
本人4／26曾來上課
部落格
圖片皆在部落中http://kaohsiungman888.blogspot.com/
===================================================================
有一組四連桿，其桿長分別為r=[4 3 3 5]，由桿2驅動，設第一固定桿角度theta1=0度; 角速度 td2=10rad/s; 角加速度tdd2=0 rad/s^2。
問題一：設桿2角度theta2=45度時，求各點之位置、速度與加速度為何？
====================================================================
依照題目的需求
輸入程式碼
[val,form]=f4bar([4 3 3 5],0,45,10,0,-1,0) %r=[4 3 3 5] (各桿之長度)theta1 =0° theta2 =45° td2 =10 (rad/sec) tdd2 =0 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。mode = -1 (閉合型)linkdrive = 0 (驅動桿為第二桿)
abs(val(:,1))
abs(val(:,2))
abs(val(:,3))
abs(val(:,4))

桿的位置 　 2(deg) 3(rad/s) 4(rad/s2)
桿I 位置( 4 , 0 ) 0(deg) 　　 0 (rad/s)　　　 0(rad/s2) 　　　
桿II 位置( 2.12 , 2.12 ) 45.0000(deg) 　10.0000(rad/s) 　 0(rad/s2)　　　
桿III 位置 ( 3.17 , 4.93 )69.4856(deg) 　　16.2681(rad/s) 　 491.4428(rad/s2) 　　　
桿IV位置 ( 3.17 , 4.93 ) 99.5246(deg) 　　4.9677(rad/s) 　　 383.6120 (rad/s2)
P點位置( 2.1213 + 2.1213i) ( 0.0212 + 0.0212i)(rad/s)( -0.2121 - 0.2121i) (rad/s2)
Q點位置( 3.1726 + 4.9311i) ( 0.0041 - 0.0245i )(rad/s)(-1.8712 - 0.4391i)(rad/s2)　　 注意:我一直排好他，但當發佈時就會亂掉好奇怪!!!
=================================================================　
問題二：繪出此四連桿之相關位置及標明各點之速度方向及大小（以程式為之)。
=================================================================
drawlinks([4 3 3 5],0,45,-1,0)

=================================================================
問題三：當桿２迴轉時，求出此組四連桿之限制角度，並繪出其位置（以程式為之）。
=================================================================
把機動學網站的function ab_angle_limits拿來利用
在直接輸入條件
[Ang1, Ang2]=fb_angle_limits([4 3 3 5],0,0)
就可以得到我們要的結果了

得到下面的結果：
Ang1(即驅動桿與x軸之間最小夾角)= 28.9550度
Ang2(即驅動桿與x軸之間最大夾角)= 331.0450度

為了得到最小角度和最大角度的圖

我嘗試輸入了28.9 28.80 28.9549..........等都得不到圖

感覺好奇怪。

當輸入drawlinks([4 3 3 5],0,29,-1,0)時得到此圖

但是當輸入drawlinks([4 3 3 5],0,331.044,-1,0)跟最大角度只差0.001度卻跑的出來耶

在輸入
drawlinks([4 3 3 5],0,29,-1,0)
drawlinks([4 3 3 5],0,331.044,-1,0)

=================================================================
問題四：設theta2=[0:20:360]，試繪出此組四連桿之重疊影像，解釋為何有些沒有值。
=================================================================
寫一個for迴圈
將老師給的條件帶入function drawlinks
程式碼如下
for theta2=0:20:360
drawlinks([4 3 3 5],0,theta2,-1,0)
end
所得到的圖有一些真的是沒有圖案因為曲桿為主動桿,θ2為輸入，然後將講義的公式簡化
r3cosθ3= r1cosθ1+r4cosθ4-r2cosθ2
r3sinθ3= r1sinθ1+r4sinθ4-r2sinθ2
帶入
其對應之係數ＡＢＣ表示如下：
A=2r1r4cosθ1-2r2r4cosθ2
B=2r1r4sinθ1-2r2r4sinθ2
C=r1²+r2²+r4²-r3²-2r1r2(cosθ1cosθ2+sinθ1sinθ2)
可得
θ4 = 2tan-1β
由於-π/2≤tan-1β≤π/2，故 -π≤θ4≤π。
值得注意的是，B²- C²+A²≥0，亦即B²+A²≥ C²才能獲得實數的根，若無法達滿足這個條件，表示所給的桿長無法構成四連桿。因此這一個不等式可作為測試四連桿是否成立的一個準則。
所以沒有值的部份，就是沒有符合上面所推導的，因為四連桿一定要滿足r2ejθ2+r3ejθ3=r1ejθ1+r4ejθ4，所以圖通所顯現的桿就代表四連桿滿足此條件，實際情形中它是真的可以轉到該角度。
其中我們可得到
Combination of links fail at degrees 0.0 20.0 340.0 360.0

==================================================================
問題五：若將問題三考慮在內，只在可迴轉的範圍內迴轉，請問你能讓此組四連桿作成動畫方式迴轉嗎？
=================================================================
pause(3) % 因為要讓我有時間準備拍影片的工具!!
title('b94611037 蔡智鴻')
for
theta=28.9551:(331.0449-28.9551)/40:331.0449%分成40等份
axis equal
axis([-4 5 -5 6]);
drawlinks([4 3 3 5],0,theta,-1,0)
pause(0.35)
clf
end
for
theta2=331.0449:-(331.0449-28.9551)/25:28.9551
title('b94611037 蔡智鴻')
axis equal
axis([-4 5 -5 6]);
drawlinks([4 3 3 5],0,theta2,-1,0)
pause(0.3)
end

作業七

我有上本週（十九日）的課。
蔡智鴻 B94611037
部落格
圖示
圖片皆在部落中http://kaohsiungman888.blogspot.com/
此次的作業中，會用到作業中的一些程式如下!
function [vec, dyadata] = dyad(rho,theta,td,tdd)
%
% function [vec, th, dyadata] = dyad(rho,theta,td,tdd)
% Analyzes a dyad linkage composing a crank and a dyad.
% Inputs: rho:length of links
% theta:incling angles, deg.
% td:angular velocity, rad/s
% tdd:angular acceleration, rad/s^2
% Outputs: vec:absoute length of links
% th:angles of links, velocities & acc, deg
% dyadata:original data, in complex forms
% Example:[vec,th,dyadata] = dyad([5 10],[30 50],[2 4])
theta=theta(:);
rho=rho(:);
n=length(rho);
if nargin<4, tdd="zeros(size(rho)); " nargin="=" td="ones(size(rho)); " td="ones(size(rho))*td; end " tdd="ones(size(rho))*tdd; end " td="td(:); tdd=" d2g="pi/180; " tt="exp(i*theta*d2g); " pp="rho.*tt; " vv="i*td.*pp; " aa="-pp.*td.^2+i*pp.*tdd; " dyadata="[pp" vec="[abs(sum(dyadata));angle(sum(dyadata))/d2g]; " x="[0;cumsum(real(data(:,1)))]; y=" i="1:length(x)-1" k="1:length(rho)" x0="x(k+1); y0=" vx="x0+real(data(k,2)); vy=" ax="x0+real(data(k,3)); ay=" sdata="sum(data); " ss="[real(sdata(1))" vv="[real(sdata(2))" aa="[real(sdata(3))" nargin="=" dd="1;end;" d="abs(dd); " ab="(B(1)+j*B(2))-(A(1)+j*A(2)); " d="abs(AB); th=" t="linspace(pi/2,2.5*pi,20); " cout="max(d/2,0.2)*exp(j*t'); Cin=">0,
P=[0;Cin;Cout(1:10);D+Cout(11:20);D+Cin;D+Cout(20);Cout(1)];
else
P=[Cin;0;D;D+Cin];
end
xx=real(P);yy=imag(P);
x=xx*cos(th)-yy*sin(th)+A(1);
y=xx*sin(th)+yy*cos(th)+A(2);
line(x,y)
axis equal

===================================================================
設有三桿相連結成端桿(dyad)之型式。請利用網路講義中之函數dyad及dyad_draw作分析。
function dyad_draw(rho,theta,td,tdd)其中：

各桿之對應長度rho=[a, a+5, a-5]cm，a=(你的學號末一碼）+10；
各桿之對應起始角度theta=[0, 0, 0]度；
各桿之對應角速度為td=[0.2, 0.5, 0 .3]rad/s；
各桿之對應角加速度為tdd=[0, 0.1, 0.2]rad/s^2；
問：

1.當t=[1 2 3 4 5]秒時，此端桿之對應
方位如何？======================================================================
因為要求t=[1 2 3 4 5]秒時，桿當時的角速度和角度，所以如果用手算就太慢的，因此我寫的一個for迴圈讓電腦幫我算!!為什麼要用for迴圈呢?因為我可以等一下直接用此回圈坐第三小題!

for n=1
axis equal;
AXIS([-200 200 -200 200]);
dyad_draw([17,22,12],[0.2,0.5+n*0.1,0.3+n*0.2],[0.2,0.5+n*0.1,0.3+n*0.2],[0,0.1,0.2]);
end;
然後n依序輸入1.2.3.4.5，即可得到此端桿之對應方位
各連桿的法線加速度以紅色線,連桿的合加速度以粉紅色線,連桿的合速度以綠色線表示。
t=0

t=1

t=2

t=3

t=4

t=5




=====================================================================
2.繪出三桿之結點之速度，加速度與時間t
之關係。
====================================================================
加速度與時間的圖在部落格中

桿一

桿二


桿三

====================================================================
3.能作出此時間區段之動畫嗎？
====================================================================
axis equal;

AXIS([-200 200 -200 200]);
dyad_draw([17,22,12],[0,0,0],[0.2,0.5,0.3],[0,0.1,0.2]);%學號B94611037最後一碼為,所以a=10+7=17

title('b94611037 蔡智鴻')
ground(0,0,5,0)
anchor(-5,0,0,0)
pause(5)
clf%叫出fuction的原因，因為要讓我有時間準備拍影片的工具!!
for n=1:5%1到5秒
axis equal;
AXIS([-200 200 -200 200]);
%theta=td*n+0.5*tdd*n*n
%td=tdd*n
%底下的theta和td都已被我化簡過
dyad_draw([17,22,12],[0.2*n,0.5*n+0.05*n*n,0.3*n+0.1*n*n],[0.2,0.5+n*0.1,0.3+n*0.2],[0,0.1,0.2]);
title('b94611037 蔡智鴻')
ground(0,0,5,0)
anchor(-5,0,0,0)
pause(2)
clf
end;

作業六

我有上本週（十二日）的課。
蔡智鴻 B94611037
部落格
圖示
圖片皆在部落中http://kaohsiungman888.blogspot.com/
此次的作業中，會用到作業中的一些程式如下!
function [df]=gruebler(nlink,jointype)
%% [df]=gruebler(nlink,jointype)
% nlink:no. of total links
% jointype:row matrix for number of joints for each type,
% the order of elements is:
% 1 R-joint 2 slider 3 compound joint(sliding & rolling)
% 4 ball 5 cylinder 6 planar 7 cylinder rolling
% 8 cam 9 helix 10 ball & 11 point contact
% Example: df=gruebler(4,[4])
% Author:D.S.Fon Bime,NTU. Date:Jan. 30, 2007
code=[1 1 2 3 2 3 1 2 1 3 5];
n=length(jointype);
dim=3;
if n>3, dim=6;
end;
ff=0;
njoint=0;
for i=1:n,
njoint=njoint+jointype(i);
ff=ff+jointype(i)*code(i);
end;
df=dim*(nlink-njoint-1)+ff;

function ans=grashof(ground_no,linkage)
% Function to test the Grashof linkage
% Inputs:
% ground_no:the ground link number in the order
% linkage: row matrix for lengths of the 4 links
% in original assigned order.
% Example:ans=grashof(4,[4 4.2 2.6 2])
% Revised: March 4, 2006
ground=linkage(ground_no);
link=sort(linkage);% sorting the links
ig=find(linkage==link(1));
if link(1)+link(4)>link(3)+link(2),
ans='Non-Grashof Linkage';
elseif link(1)+link(4)==link(3)+link(2)
ans='Neutral Linkage';
elseif link(1)==ground,
ans='Double-Crank Linkage';
else
switch ig
case 1
im=3;
case 2
im=4;
case 3
im=1;
case 4
im=2;
end
if ground==linkage(im)
ans='Double-Rocker Linkage';
else
ans='Crank-Rocker Linkage';
end
end
然後作業問題回答如下
===================================================================
６.1某一平面組合機構如下圖，其中包括兩滑塊元件一與地固定，另一分於固定於兩桿。青色者則為滑槽。
試 標出桿號及結數，並計算共計有多少連桿及結數。
利用古魯伯公式，計算此機構之可動度，請列出其計算方法。
請利用function[df]=gruebler()函數計算其對應之可動度。
討論此機構中滑塊及滑槽對可動度之影響。
===================================================================
6.1.1
共有12桿及15個結
而12桿及15個結的詳細編號皆在我的部落格


6.1.2 古魯伯公式計算機構之可動度
M=3*(N-J-1)+F
其中
F為2個滑槽結+12個旋轉結+1個滑動結
F=12*1+1*1+2*2=17
N=12　J=15　
M=-12+17=5　
所以自由度為5
6.1.3 matlab計算其對應之可動度
輸入
gruebler(12,[12 1 2])
可以得到自由度為5
6.1.4
因為滑塊會和地面間的有滑動特性，使整個系統多出了一個滑動結。
因為滑槽因為可以上下滑動與和轉動的自由度，所以滑槽自由度為2。
===================================================================
６.2 下面為一個立體機構,分別由兩個旋轉結，一個筒結及三個球結組成。試說明：
各結之自由度如何？
利用古魯伯公式如何計算整個機構之自由度，可以動嗎？
請利用function[df]=gruebler()函數計算其對應之可動度，並相互印證。
這裡有所謂楕性自由度嗎？其對整個機構之影響如何？
===================================================================
6.2.1
如圖片所式


　a,b,c為球結，自由度為3
　d,e 為旋轉結，自由度為1
　f 為圓柱結，自由度為2
6.2.2 古魯伯公式計算機構之可動度
　F=3*3+2*1+1*2=13
　M=6(N-J-1)+F=6(6-6-1)+13
　M=7　
自由度為7
6.2.3 matlab計算其對應之可動度
　輸入
　gruebler(6,[2 0 0 3 1])
可以得到自由度為7
6.2.4
　經觀察本題是有惰性自由度的，因為圖中的4號桿與6號桿可以自轉，所以惰性自由度為2。總自由度為7-2=5
===================================================================
６.3

何謂葛拉索機構及非葛拉索機構?
假設有三組四連桿，設第一桿為固定桿，各桿長度分別如下：
第一組：桿1-桿4分別為7,4,6,5cm
第二組：桿1-桿4分別為8,3.6,5.1,4.1cm
第三組：桿1-桿4分別為5.4,3.1,6.6,4.7cm
試問各組應屬何種機構？其迴轉情況會如何？
試用grashof()函數檢驗上述三組的連桿組合。
上述三組連桿若要成為葛拉索機構，則應如何改善？
===================================================================
6.3.1 何謂葛拉索機構及非葛拉索機構?
1.葛拉索第一類型，亦稱為葛拉索型:在一四連桿組中，最短桿與最長桿之和小於其他兩桿之和時，則至少有一桿為可旋轉桿。
2.葛拉索第二類型，或稱為非葛拉索型:
最短桿與最長桿之和大於其他兩桿之和時，所有的活動連桿必為搖桿
即一四連桿當中，令四桿的桿長為g:最長桿的長度ｓ:最短桿的長度p,q:中間長度之兩桿的長度則當s+g＜p+q時，為葛拉索第一類型。s+g＞p+q，為葛拉索第二類型。s+g=p+q，為葛拉索第三類型
6.3.2
第一組中，7+4=6+5，所以是屬於葛拉索第三類桿，即是中立連桿組
　
輸入
grashof(1,[7 4 6 5])
ans =Neutral Linkage

第二組中，8+3.6>5.1+4.1，屬於葛索 第二類桿　
輸入
grashof(1,[8 3.6 5.1 4.1])
ans =Non-Grashof Linkage

第三組中，6.6+3.1<5.4+4.7，屬於葛拉索第一類桿>
輸入 grashof(1,[5.4 3.1 6.6 4.7])
ans =Crank-Rocker Linkage
6.3.3 　
觀察上面三個問題的答案，只有第二組四連桿為非葛拉索型，若要將第一組改成葛拉索型機構，我們可以把它的最常和最短的桿減短，然後將次長和次短的桿長度增加，以達成葛拉索機構最長與最短之和小於另外兩桿之和的要求。

作業五

B94611037 蔡智鴻
部落格http://kaohsiungman888.blogspot.com/圖片皆在部落格中
第一小題
L1=35;%這是上手臂長
L2=30;%這是手臂長
L3=8;%這是手掌長
r1=L1/6;%把手掌分段以利設座標
r2=L2/2;
r3=L3/2;
a1=[0 r1*cosd(150)+r1 r1*cosd(120)+r1 r1 r1*cosd(60)+r1 r1*cosd(30)+r1 2*r1*cosd(45)+r1 2*r1*cosd(60)+2*r1 4*r1 2*r1*cosd(60)+4*r1 2*r1*cosd(45)+4*r1 6*r1 2*r1*cosd(45)+4*r1 2*r1*cosd(60)+4*r1 4*r1 2*r1*cosd(60)+2*r1 2*r1*cosd(45)+r1 r1*cosd(30)+r1 r1*cosd(60)+r1 r1 r1*cosd(240)+r1 r1*cosd(210)+r1 0 L1];
b1=[0 r1*sind(150) r1*sind(120) r1 r1*sind(60) r1*sind(30) r1*sind(45) r1*sind(60) r1 r1*sind(60) r1*sind(45) 0 -r1*sind(45) -r1*sind(60) -r1 -r1*sind(60) -r1*sind(45) -r1*sind(30) -r1*sind(60) -r1 r1*sind(240) r1*sind(210) 0 0];
a2=[0 r2+r2*cosd(150) r2+r2*cosd(120) r2+r2*cosd(90) r2+r2*cosd(60) r2+r2*cosd(30) r2+r2*cosd(0) r2+r2*cosd(30) r2+r2*cosd(60) r2+r2*cosd(90) r2+r2*cosd(120) r2+r2*cosd(150) 0 2*r2];
b2=[0 r2/5*sind(150) r2/5*sind(120) r2/5*sind(90) r2/5*sind(60) r2/5*sind(30) r2/5*sind(0) -r2/5*sind(30) -r2/5*sind(60) -r2/5*sind(90) -r2/5*sind(120) -r2/5*sind(150) 0 0 ];
a3=[0 0 r3/2 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 0 0 2*r3];
b3=[0 r3*1.5 r3*1.5 r3 r3 r3/2 r3/2 r3/2 0 0 0 -r3/2 -r3/2 -r3/2 -r3 -r3 0 0 ];
axis equal
line(a1,b1); %把座標連接起來
line(a2,b2);
line(a3,b3);
clf
theta1=90;theta2=-45;theta3=-30;
axis equal
AXIS([-25 35 -50 30]);
x1=a1*cosd(-theta1)-b1*sind(-theta1); %以下都是旋轉和平移目的是轉動和連接各部份
y1=a1*sind(-theta1)+b1*cosd(-theta1);
line(x1,y1)
theta2=180+theta1-theta2;
x2=a2*cosd(-theta2)-b2*sind(-theta2)+x1(12);
y2=a2*sind(-theta2)+b2*cosd(-theta2)+y1(12);
line(x2,y2)theta3=180+theta2-theta3;
x3=a3*cosd(-theta3)-b3*sind(-theta3)+x2(7);
y3=a3*sind(-theta3)+b3*cosd(-theta3)+y2(7);
line(x3,y3)



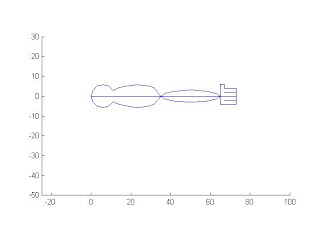
第2小題
function body1(L1,L2,L3,theta1,theta2,theta3)
r1=L1/6;%把手掌分段以利設座標
r2=L2/2;
r3=L3/2;
a1=[0 r1*cosd(150)+r1 r1*cosd(120)+r1 r1 r1*cosd(60)+r1 r1*cosd(30)+r1 2*r1*cosd(45)+r1 2*r1*cosd(60)+2*r1 4*r1 2*r1*cosd(60)+4*r1 2*r1*cosd(45)+4*r1 6*r1 2*r1*cosd(45)+4*r1 2*r1*cosd(60)+4*r1 4*r1 2*r1*cosd(60)+2*r1 2*r1*cosd(45)+r1 r1*cosd(30)+r1 r1*cosd(60)+r1 r1 r1*cosd(240)+r1 r1*cosd(210)+r1 0 L1]; %這是上手臂座標
b1=[0 r1*sind(150) r1*sind(120) r1 r1*sind(60) r1*sind(30) r1*sind(45) r1*sind(60) r1 r1*sind(60) r1*sind(45) 0 -r1*sind(45) -r1*sind(60) -r1 -r1*sind(60) -r1*sind(45) -r1*sind(30) -r1*sind(60) -r1 r1*sind(240) r1*sind(210) 0 0]; %這是上手臂座標
a2=[0 r2+r2*cosd(150) r2+r2*cosd(120) r2+r2*cosd(90) r2+r2*cosd(60) r2+r2*cosd(30) r2+r2*cosd(0) r2+r2*cosd(30) r2+r2*cosd(60) r2+r2*cosd(90) r2+r2*cosd(120) r2+r2*cosd(150) 0 2*r2];
b2=[0 r2/5*sind(150) r2/5*sind(120) r2/5*sind(90) r2/5*sind(60) r2/5*sind(30) r2/5*sind(0) -r2/5*sind(30) -r2/5*sind(60) -r2/5*sind(90) -r2/5*sind(120) -r2/5*sind(150) 0 0 ];
a3=[0 0 r3/2 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 0 0 2*r3]; %這是手掌座標
b3=[0 r3*1.5 r3*1.5 r3 r3 r3/2 r3/2 r3/2 0 0 0 -r3/2 -r3/2 -r3/2 -r3 -r3 0 0 ]; %這是手掌座標
axis equal
line(a1,b1);%把座標連接起來
line(a2,b2);
line(a3,b3);
clf
axis equal
AXIS([-25 35 -50 30]);
x1=a1*cosd(-theta1)-b1*sind(-theta1); %以下都是旋轉和平移目的是轉動和連接各部份
y1=a1*sind(-theta1)+b1*cosd(-theta1);
line(x1,y1)theta2=180+theta1-theta2;
x2=a2*cosd(-theta2)-b2*sind(-theta2)+x1(12);
y2=a2*sind(-theta2)+b2*cosd(-theta2)+y1(12);
line(x2,y2)theta3=180+theta2-theta3;
x3=a3*cosd(-theta3)-b3*sind(-theta3)+x2(7);
y3=a3*sind(-theta3)+b3*cosd(-theta3)+y2(7);
line(x3,y3)

第3小題

從新開一個檔案然後把function body1(L1,L2,L3,theta1,theta2,theta3)填入所需要的值所以新檔案打上下面的式子即可body1(35,30,8,90,-45,-35)



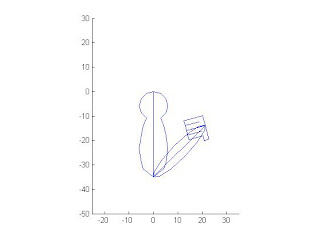
第4小題
L1=35;%這是上手臂長
L2=30;%這是手臂長
L3=8;%這是手掌長
r1=L1/6;%把手掌分段以利設座標
r2=L2/2;
r3=L3/2;
a1=[0 r1*cosd(150)+r1 r1*cosd(120)+r1 r1 r1*cosd(60)+r1 r1*cosd(30)+r1 2*r1*cosd(45)+r1 2*r1*cosd(60)+2*r1 4*r1 2*r1*cosd(60)+4*r1 2*r1*cosd(45)+4*r1 6*r1 2*r1*cosd(45)+4*r1 2*r1*cosd(60)+4*r1 4*r1 2*r1*cosd(60)+2*r1 2*r1*cosd(45)+r1 r1*cosd(30)+r1 r1*cosd(60)+r1 r1 r1*cosd(240)+r1 r1*cosd(210)+r1 0 L1]; %這是上手臂座標
b1=[0 r1*sind(150) r1*sind(120) r1 r1*sind(60) r1*sind(30) r1*sind(45) r1*sind(60) r1 r1*sind(60) r1*sind(45) 0 -r1*sind(45) -r1*sind(60) -r1 -r1*sind(60) -r1*sind(45) -r1*sind(30) -r1*sind(60) -r1 r1*sind(240) r1*sind(210) 0 0]; %這是上手臂座標
a2=[0 r2+r2*cosd(150) r2+r2*cosd(120) r2+r2*cosd(90) r2+r2*cosd(60) r2+r2*cosd(30) r2+r2*cosd(0) r2+r2*cosd(30) r2+r2*cosd(60) r2+r2*cosd(90) r2+r2*cosd(120) r2+r2*cosd(150) 0 2*r2]; %這是手臂座標
b2=[0 r2/5*sind(150) r2/5*sind(120) r2/5*sind(90) r2/5*sind(60) r2/5*sind(30) r2/5*sind(0) -r2/5*sind(30) -r2/5*sind(60) -r2/5*sind(90) -r2/5*sind(120) -r2/5*sind(150) 0 0 ]; %這是手臂座標
a3=[0 0 r3/2 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 r3/2 2*r3 2*r3 0 0 2*r3]; %這是手掌座標
b3=[0 r3*1.5 r3*1.5 r3 r3 r3/2 r3/2 r3/2 0 0 0 -r3/2 -r3/2 -r3/2 -r3 -r3 0 0 ];%這是手掌座標
axis equal
line(a1,b1); %把座標連接起來
line(a2,b2);
line(a3,b3);
clf
theta1=linspace(-90,-75,10) %-90和-75度之間分十等分
theta2=linspace(-45,-35,10) %-45和-35度之間分十等分
theta3=linspace(-30,-10,10) %-30和-10度之間分十等分
for n=1:25;
axis equal
AXIS([-100 100 -100 100]);
x1=a1*cosd(-theta1(n))-b1*sind(-theta1(n)); %以下都是旋轉和平移目的是轉動和連接各部份
y1=a1*sind(-theta1(n))+b1*cosd(-theta1(n));
line(x1,y1)theta2(n)=180+theta1(n)-theta2(n);
x2=a2*cosd(-theta2(n))-b2*sind(-theta2(n))+x1(12);
y2=a2*sind(-theta2(n))+b2*cosd(-theta2(n))+y1(12);
line(x2,y2)theta3(n)=180+theta2(n)-theta3(n);
x3=a3*cosd(-theta3(n))-b3*sind(-theta3(n))+x2(7);
y3=a3*sind(-theta3(n))+b3*cosd(-theta3(n))+y2(7);
line(x3,y3)
pause(0.05)
clf
end;

http://www.youtube.com/watch?v=_VgMcEDvl7k
5.2.1
假設指夾部分是L1，下一截是L2，接手掌部分是L3。L1、L2和L2跟手掌之間只能旋轉90度的旋轉節，L2、L3亦有90度的限制。　　套用自由度計算因為有三個節，節之自由度總和為1+1+1=3　
5.2.2

食指
function hand1(P,theta1,theta2,theta3)
Ltotal=P %這是輸入你的手掌長
L1=5/18*Ltotal;%這是連接手掌的長度
L2=3/18*Ltotal;%這是中間部分
L3=2.5/18*Ltotal;%這是指夾的長度
r1=L1/2;
r2=L2/2;
r3=L3/2;
a1=[0 r1+r1*cosd(150) r1+r1*cosd(120) r1+r1*cosd(90) r1+r1*cosd(60) r1+r1*cosd(30) r1+r1*cosd(0) r1+r1*cosd(30) r1+r1*cosd(60) r1+r1*cosd(90) r1+r1*cosd(120) r1+r1*cosd(150) 0 2*r1];%這是連接手掌的座標
b1=[0 r1/5*sind(150) r1/5*sind(120) r1/5*sind(90) r1/5*sind(60) r1/5*sind(30) r1/5*sind(0) -r1/5*sind(30) -r1/5*sind(60) -r1/5*sind(90) -r1/5*sind(120) -r1/5*sind(150) 0 0 ];
a2=[0 r2+r2*cosd(150) r2+r2*cosd(120) r2+r2*cosd(90) r2+r2*cosd(60) r2+r2*cosd(30) r2+r2*cosd(0) r2+r2*cosd(30) r2+r2*cosd(60) r2+r2*cosd(90) r2+r2*cosd(120) r2+r2*cosd(150) 0 2*r2];%這是中間部分部份
b2=[0 r2/5*sind(150) r2/5*sind(120) r2/5*sind(90) r2/5*sind(60) r2/5*sind(30) r2/5*sind(0) -r2/5*sind(30) -r2/5*sind(60) -r2/5*sind(90) -r2/5*sind(120) -r2/5*sind(150) 0 0 ];
a3=[0 r3+r3*cosd(150) r3+r3*cosd(120) r3+r3*cosd(90) r3+r3*cosd(60) r3+r3*cosd(30) r3+r3*cosd(0) r3+r3*cosd(30) r3+r3*cosd(60) r3+r3*cosd(90) r3+r3*cosd(120) r3+r3*cosd(150) 0 2*r3];%這是指夾的座標
b3=[0 r3/5*sind(150) r3/5*sind(120) r3/5*sind(90) r3/5*sind(60) r3/5*sind(30) r3/5*sind(0) -r3/5*sind(30) -r3/5*sind(60) -r3/5*sind(90) -r3/5*sind(120) -r3/5*sind(150) 0 0 ];
axis equal
AXIS([-10 10 -10 10])
line(a1,b1);
line(a2,b2);
line(a3,b3);
axis equal
x1=a1*cosd(-theta1)-b1*sind(-theta1);%這是連接各部份手指的部份
y1=a1*sind(-theta1)+b1*cosd(-theta1);
line(x1,y1)theta2=180+theta1-theta2;
x2=a2*cosd(-theta2)-b2*sind(-theta2)+x1(7);
y2=a2*sind(-theta2)+b2*cosd(-theta2)+y1(7);
line(x2,y2)theta3=180+theta2-theta3;
x3=a3*cosd(-theta3)-b3*sind(-theta3)+x2(14);
y3=a3*sind(-theta3)+b3*cosd(-theta3)+y2(14);line(x3,y3)


然後開一個新檔呼叫function
檔案如下
theta1=linspace(0,90,10);
theta2=linspace(180,90,10);
theta3=linspace(180,90,10);
for n=1:10
hand1(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end





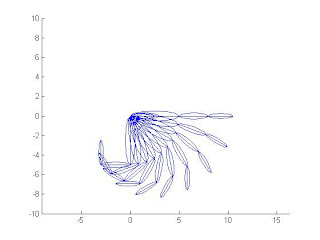
中指
function hand2(P,theta1,theta2,theta3)
Ltotal=P %這是輸入你的手掌長
L1=5/18*Ltotal;%這是連接手掌的長度
L2=3/18*Ltotal;%這是中間部分
L3=2.5/18*Ltotal;%這是指夾的長度
r1=L1/2;
r2=L2/2;
r3=L3/2;
a1=[0 r1+r1*cosd(150) r1+r1*cosd(120) r1+r1*cosd(90) r1+r1*cosd(60) r1+r1*cosd(30) r1+r1*cosd(0) r1+r1*cosd(30) r1+r1*cosd(60) r1+r1*cosd(90) r1+r1*cosd(120) r1+r1*cosd(150) 0 2*r1];%這是連接手掌的座標
b1=[0 r1/5*sind(150) r1/5*sind(120) r1/5*sind(90) r1/5*sind(60) r1/5*sind(30) r1/5*sind(0) -r1/5*sind(30) -r1/5*sind(60) -r1/5*sind(90) -r1/5*sind(120) -r1/5*sind(150) 0 0 ];
a2=[0 r2+r2*cosd(150) r2+r2*cosd(120) r2+r2*cosd(90) r2+r2*cosd(60) r2+r2*cosd(30) r2+r2*cosd(0) r2+r2*cosd(30) r2+r2*cosd(60) r2+r2*cosd(90) r2+r2*cosd(120) r2+r2*cosd(150) 0 2*r2];%這是中間部分部份
b2=[0 r2/5*sind(150) r2/5*sind(120) r2/5*sind(90) r2/5*sind(60) r2/5*sind(30) r2/5*sind(0) -r2/5*sind(30) -r2/5*sind(60) -r2/5*sind(90) -r2/5*sind(120) -r2/5*sind(150) 0 0 ];a3=[0 r3+r3*cosd(150) r3+r3*cosd(120) r3+r3*cosd(90) r3+r3*cosd(60) r3+r3*cosd(30) r3+r3*cosd(0) r3+r3*cosd(30) r3+r3*cosd(60) r3+r3*cosd(90) r3+r3*cosd(120) r3+r3*cosd(150) 0 2*r3];%這是指夾的座標
b3=[0 r3/5*sind(150) r3/5*sind(120) r3/5*sind(90) r3/5*sind(60) r3/5*sind(30) r3/5*sind(0) -r3/5*sind(30) -r3/5*sind(60) -r3/5*sind(90) -r3/5*sind(120) -r3/5*sind(150) 0 0 ];
axis equal
AXIS([-10 10 -10 10])
line(a1,b1);
line(a2,b2);
line(a3,b3);
axis equal
x1=a1*cosd(-theta1)-b1*sind(-theta1);%這是連接各部份手指的部份
y1=a1*sind(-theta1)+b1*cosd(-theta1);
line(x1,y1)theta2=180+theta1-theta2;
x2=a2*cosd(-theta2)-b2*sind(-theta2)+x1(7);
y2=a2*sind(-theta2)+b2*cosd(-theta2)+y1(7);
line(x2,y2)theta3=180+theta2-theta3;
x3=a3*cosd(-theta3)-b3*sind(-theta3)+x2(14);
y3=a3*sind(-theta3)+b3*cosd(-theta3)+y2(14);
line(x3,y3)
然後開一個新檔呼叫function
檔案如下
theta1=linspace(0,90,10);
theta2=linspace(180,90,10);
theta3=linspace(180,90,10);
for n=1:10
hand2(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end





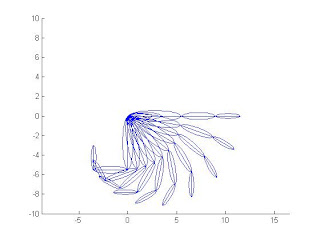
無名指
function hand3(P,theta1,theta2,theta3)
Ltotal=P %這是輸入你的手掌長
L1=5/18*Ltotal;%這是連接手掌的長度
L2=3/18*Ltotal;%這是中間部分
L3=2.5/18*Ltotal;%這是指夾的長度
r1=L1/2;
r2=L2/2;
r3=L3/2;
a1=[0 r1+r1*cosd(150) r1+r1*cosd(120) r1+r1*cosd(90) r1+r1*cosd(60) r1+r1*cosd(30) r1+r1*cosd(0) r1+r1*cosd(30) r1+r1*cosd(60) r1+r1*cosd(90) r1+r1*cosd(120) r1+r1*cosd(150) 0 2*r1];%這是連接手掌的座標
b1=[0 r1/5*sind(150) r1/5*sind(120) r1/5*sind(90) r1/5*sind(60) r1/5*sind(30) r1/5*sind(0) -r1/5*sind(30) -r1/5*sind(60) -r1/5*sind(90) -r1/5*sind(120) -r1/5*sind(150) 0 0 ];
a2=[0 r2+r2*cosd(150) r2+r2*cosd(120) r2+r2*cosd(90) r2+r2*cosd(60) r2+r2*cosd(30) r2+r2*cosd(0) r2+r2*cosd(30) r2+r2*cosd(60) r2+r2*cosd(90) r2+r2*cosd(120) r2+r2*cosd(150) 0 2*r2];%這是中間部分部份
b2=[0 r2/5*sind(150) r2/5*sind(120) r2/5*sind(90) r2/5*sind(60) r2/5*sind(30) r2/5*sind(0) -r2/5*sind(30) -r2/5*sind(60) -r2/5*sind(90) -r2/5*sind(120) -r2/5*sind(150) 0 0 ];
a3=[0 r3+r3*cosd(150) r3+r3*cosd(120) r3+r3*cosd(90) r3+r3*cosd(60) r3+r3*cosd(30) r3+r3*cosd(0) r3+r3*cosd(30) r3+r3*cosd(60) r3+r3*cosd(90) r3+r3*cosd(120) r3+r3*cosd(150) 0 2*r3];%這是指夾的座標
b3=[0 r3/5*sind(150) r3/5*sind(120) r3/5*sind(90) r3/5*sind(60) r3/5*sind(30) r3/5*sind(0) -r3/5*sind(30) -r3/5*sind(60) -r3/5*sind(90) -r3/5*sind(120) -r3/5*sind(150) 0 0 ];
axis equal
AXIS([-10 10 -10 10])
line(a1,b1);
line(a2,b2);
line(a3,b3);
axis equal
x1=a1*cosd(-theta1)-b1*sind(-theta1);%這是連接各部份手指的部份
y1=a1*sind(-theta1)+b1*cosd(-theta1);
line(x1,y1)
theta2=180+theta1-theta2;
x2=a2*cosd(-theta2)-b2*sind(-theta2)+x1(7);
y2=a2*sind(-theta2)+b2*cosd(-theta2)+y1(7);
line(x2,y2)
theta3=180+theta2-theta3;
x3=a3*cosd(-theta3)-b3*sind(-theta3)+x2(14);
y3=a3*sind(-theta3)+b3*cosd(-theta3)+y2(14);
line(x3,y3)(-theta3)+y2(14);
line(x3,y3)

然後開一個新檔呼叫function
檔案如下
theta1=linspace(0,90,10);
theta2=linspace(180,90,10);
theta3=linspace(180,90,10);
for n=1:10
hand1(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end



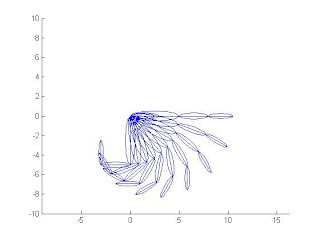
小拇指

function hand4(P,theta1,theta2,theta3)
Ltotal=P %這是輸入你的手掌長
L1=5/18*Ltotal;%這是連接手掌的長度
L2=3/18*Ltotal;%這是中間部分
L3=2.5/18*Ltotal;%這是指夾的長度
r1=L1/2;
r2=L2/2;
r3=L3/2;
a1=[0 r1+r1*cosd(150) r1+r1*cosd(120) r1+r1*cosd(90) r1+r1*cosd(60) r1+r1*cosd(30) r1+r1*cosd(0) r1+r1*cosd(30) r1+r1*cosd(60) r1+r1*cosd(90) r1+r1*cosd(120) r1+r1*cosd(150) 0 2*r1];%這是連接手掌的座標
b1=[0 r1/5*sind(150) r1/5*sind(120) r1/5*sind(90) r1/5*sind(60) r1/5*sind(30) r1/5*sind(0) -r1/5*sind(30) -r1/5*sind(60) -r1/5*sind(90) -r1/5*sind(120) -r1/5*sind(150) 0 0 ];
a2=[0 r2+r2*cosd(150) r2+r2*cosd(120) r2+r2*cosd(90) r2+r2*cosd(60) r2+r2*cosd(30) r2+r2*cosd(0) r2+r2*cosd(30) r2+r2*cosd(60) r2+r2*cosd(90) r2+r2*cosd(120) r2+r2*cosd(150) 0 2*r2];%這是中間部分部份
b2=[0 r2/5*sind(150) r2/5*sind(120) r2/5*sind(90) r2/5*sind(60) r2/5*sind(30) r2/5*sind(0) -r2/5*sind(30) -r2/5*sind(60) -r2/5*sind(90) -r2/5*sind(120) -r2/5*sind(150) 0 0 ];
a3=[0 r3+r3*cosd(150) r3+r3*cosd(120) r3+r3*cosd(90) r3+r3*cosd(60) r3+r3*cosd(30) r3+r3*cosd(0) r3+r3*cosd(30) r3+r3*cosd(60) r3+r3*cosd(90) r3+r3*cosd(120) r3+r3*cosd(150) 0 2*r3];%這是指夾的座標
b3=[0 r3/5*sind(150) r3/5*sind(120) r3/5*sind(90) r3/5*sind(60) r3/5*sind(30) r3/5*sind(0) -r3/5*sind(30) -r3/5*sind(60) -r3/5*sind(90) -r3/5*sind(120) -r3/5*sind(150) 0 0 ];
axis equal
AXIS([-10 10 -10 10])
line(a1,b1);
line(a2,b2);
line(a3,b3);
axis equal
x1=a1*cosd(-theta1)-b1*sind(-theta1);%這是連接各部份手指的部份
y1=a1*sind(-theta1)+b1*cosd(-theta1);
line(x1,y1)
theta2=180+theta1-theta2;
x2=a2*cosd(-theta2)-b2*sind(-theta2)+x1(7);
y2=a2*sind(-theta2)+b2*cosd(-theta2)+y1(7);
line(x2,y2)
theta3=180+theta2-theta3;
x3=a3*cosd(-theta3)-b3*sind(-theta3)+x2(14);
y3=a3*sind(-theta3)+b3*cosd(-theta3)+y2(14);
line(x3,y3)

然後開一個新檔呼叫function
檔案如下
theta1=linspace(0,90,10);
theta2=linspace(180,90,10);
theta3=linspace(180,90,10);
for n=1:10
hand1(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end







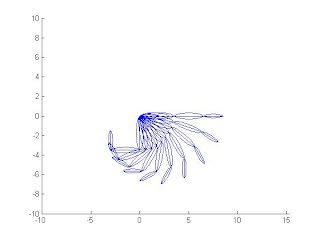
然後開一個新檔呼叫function
檔案如下
theta1=linspace(0,90,10);
theta2=linspace(180,90,10);
theta3=linspace(180,90,10);
for n=1:10
hand1(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end
for n=1:10
hand2(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end
for n=1:10
hand3(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end
for n=1:10
hand4(18,theta1(n),theta2(n),theta3(n))
pause(0.05)
end


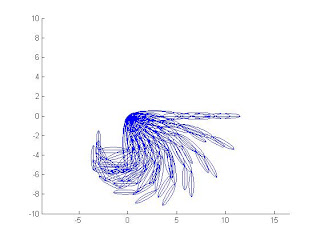
5.2.3假設球投出的瞬間，手掌和接手掌指節的角速度是和角加速度是W和a
然後指節長度是R
所以切線加速度就是aR
而法線加速度就是w*w*R

作業四

B94611037 蔡智鴻

作業4-1

以講義第二章之圖2.5之正三角形為例,試寫出matlab程式，分別就三個頂點作動態旋轉(正三角形之邊長L=(你的學號末二碼)+10)。

L=37+10;

axis equal;

AXIS([-200 200 -200 200])

x=[0 L/2 L 0];

y=[0 (3)^(1/2)*L/2 0 0];

picture=line(x,y)

for n=1:120

rotate(picture,[0 0 1],3,[ L/2 (3)^(1/2)*L/2 0])

pause(0.005)
end

for n=1:120

rotate(picture,[0 0 1],3,[L 0 0])

pause(0.005)

end

for n=1:120

rotate(picture,[0 0 1],3,[0 0 0])

pause(0.005)

end

其實它是會動的!!!!

作業4-2

設一連桿長度為10cm，厚度為4cm，繞於原點旋轉，其另一端則以一條彈簧固定於(15,0)cm的位置，試利用matlab寫出一程式，並繪圖顯示出該桿迴轉一圈時之位置。
linkshape([10 0],[0,0],4)

axis equal;

AXIS([-25 25 -25 25])

x=10;y=0;

x1=15;y1=0;

for n=1:15:360;

x2=x*cosd(n);

y2=-x*sind(n);

linkshape([0,0], [x2,y2], 4)

line([x1,x2],[y1,y2]);

end

作業4-3

有一四連桿，其ＡＢＣＤ四點之座標分別為A(0,0);B(3,4);C(13,4);D(10,0)，其單位為cm，若ＡＤ為固定桿，ＡＢ為第二桿ＢＣ與ＣＤ分別為第三與第四桿，各桿厚度分別為2cm,3cm,1.5cm,2cm。試繪出其相關位置。

若ＡＢ為主動迴轉桿，則其每間隔30度間之對應位置會如何？

axis equal;

AXIS([-10 20 -10 10])

Ax=0;Ay=0;

Bx=3;By=4;

Cx=13;Cy=4;

Dx=10;Dy=0;

linkshape([Ax,Ay],[Bx By],2);

linkshape([Bx,By],[Cx Cy],3);

linkshape([Cx,Cy],[Dx Dy],1.5);

linkshape([Ax Ay],[Dx,Dy],2);
for n=0:20:360;

a=Bx*cosd(n)+By*sind(n);

b=-Bx*sind(n)+By*cosd(n);

c=Cx+(a-Bx);

d=b;

linkshape([a b],[Ax,Ay],2);

linkshape([c d],[a,b],3);

linkshape([Dx Dy],[c,d],1.5);

linkshape([Ax Ay],[Dx,Dy],2);

end;